Dados: 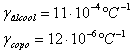
2. Um recipiente de vidro. com a capacidade de 3000cm³, está completamente cheio com líquido, a 0°C. O conjunto é aquecido até 100°C e observa-se que 15cm³ desse líquido extravasa do recipiente.
Considerando-se o coeficiente de dilatação linear do vidro como sendo constante no referido intervalo térmico e igual a 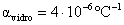 , qual o coeficiente de dilatação real desse líquido?
, qual o coeficiente de dilatação real desse líquido?
Sabendo que
E que:
De modo que podemos calcular o coeficiente de dilatação aparente do líquido e descobrir o coeficiente de dilatação real, ou seja:
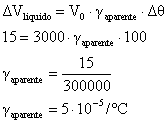
3. U
m frasco de vidro, cujo o volume é de 300 cm³ a 10°C, está completamente cheio
de um certo líquido. Qando se aquece o conjunto a uma temperatura de 140°C, transbordam 2 cm³ do líquido. Sendo o coeficiente de dilatação volumétrica do frasco
igual a 0,00027/°C, determine:
b) É só utilizar a primeira fórmula:
(Vf-Vo)real = (Vf-Vo)aparente + (Vf-Vo)frasco
Vo.Yreal.(tf-to)= 2cm³ + Vo.Yfrasco.(tf-to)
300.Yreal.(140-10)=2+300.0,00027.(140-10...
300.Yreal.130=2+0,081.130
39000Yreal=2+10,53
39000Yreal=12,53
Yreal=12,53/39000
Yreal=0,000321282...°C-¹
Ou Yreal=3,2.10^ -4°C-¹
4. Um recipiente com capacidade de 100 litros está completamente cheio de um líquido de coeficiente de dilatação térmica volumétrica 2 • 10 elevado a 5 ºC-¹ à temperapura de 10 ºC. O coeficiente de dilatação volumétrica térmica do material que constitui o recipiente é de 1•10 elevado a menos 5 ºC-¹. Calcule o volume de líquido transbordado, caso o conjunto seja aquecido a 110 ºC
vamos transformar de litros para cm³
1cm³-------0,01L
xcm³-------100L 100L=10000cm³
Primeiro temos de levar em conta que:
ΔVreal=ΔVrec+ΔVlíq
Calculemos então o ΔVlíq primeiramente.
ΔV=Vᴏ x ϫ x ΔT
Onde:
ΔV=Variação do volume
Vᴏ=Volume inicial
ϫ=Coeficiente de ditatação volumétrica
ΔT=Variação de temperatura
Fazendo as devidas substituições:
ΔV=Vᴏ x ϫ x ΔT
ΔV=10000 x 2 x 10^-5 x (110-10)
ΔV=10000 x 2 x 10^-5 x 100
ΔV= 10^4 x 10^2 x 2 x 10^-5
ΔV=2 x 10^1 ou 20cm³
Agora apliquemos a fórmula para calcular o ΔV do recipiente
ΔV=Vᴏ x ϫ x ΔT
Onde:
ΔV=Variação do volume
Vᴏ=Volume inicial
ϫ=Coeficiente de ditatação volumétrica
ΔT=Variação de temperatura
Para obtermos o ΔVrec (Do recipiente)
ΔV=Vᴏ x ϫ x ΔT
ΔV=10000 x 1 x 10^-5 x (110-10)
ΔV=10000 x 1 x 10^-5 x 100
1cm³-------0,01L
xcm³-------100L 100L=10000cm³
Primeiro temos de levar em conta que:
ΔVreal=ΔVrec+ΔVlíq
Calculemos então o ΔVlíq primeiramente.
ΔV=Vᴏ x ϫ x ΔT
Onde:
ΔV=Variação do volume
Vᴏ=Volume inicial
ϫ=Coeficiente de ditatação volumétrica
ΔT=Variação de temperatura
Fazendo as devidas substituições:
ΔV=Vᴏ x ϫ x ΔT
ΔV=10000 x 2 x 10^-5 x (110-10)
ΔV=10000 x 2 x 10^-5 x 100
ΔV= 10^4 x 10^2 x 2 x 10^-5
ΔV=2 x 10^1 ou 20cm³
Agora apliquemos a fórmula para calcular o ΔV do recipiente
ΔV=Vᴏ x ϫ x ΔT
Onde:
ΔV=Variação do volume
Vᴏ=Volume inicial
ϫ=Coeficiente de ditatação volumétrica
ΔT=Variação de temperatura
Para obtermos o ΔVrec (Do recipiente)
ΔV=Vᴏ x ϫ x ΔT
ΔV=10000 x 1 x 10^-5 x (110-10)
ΔV=10000 x 1 x 10^-5 x 100
ΔV=10^4 x 1 x 10^-5 x 10^2
ΔV=1 x 10^1 ou 10cm³
Voltemos a fórmula:ΔVreal=ΔVrec+ΔVlíq
ΔVreal=10cm³ +20cm³
ΔVreal=30cm³
ΔVreal=30cm³
b. O coeficiente de dilatação volumétrica real do líquido
Resolução:
Vamos responder esta questão utilizando a seguinte fórmula:
(Vf-Vo)real = (Vf-Vo)aparente + (Vf-Vo)frasco
Obs: (Vf-Vo) é a variação de volume(Delta) coloquei assim porque não sei como colocar aqui o triângulo representativo.
Da dilatação de líquidos contidos em um recipiente sabemos que o volume extravasado é o (Vf-Vo)aparente que no caso vale 2cm³.
a) (Vf-Vo)aparente = Vo.Yaparente.(tf-to)
2cm³ = 300cm³.Yaparente.(140°C-10°C)
2/300 = Yaparente.130
1/150 = Yaparente.130
Yaparente=1/(150.130)
Yaparente=1/19500
Yaparente=0,000051282...°C-¹
Yaparente=5,13.10^ -5°C-¹
Este comentário foi removido pelo autor.
ResponderExcluirO 3º num ta faltando alguma coisa nao, tipo desorganizado ?? determine: .... ? letra "b"? nao identifiquei o que a questao qer ;/ .. mas as outras me ajudaram muito ;)
ResponderExcluirEm ''questões sobre dilatação dos liquidos'' na 2ª questão , a resposta é só '' 5 . 10(elevado a menos cinco) / ºC ?
ResponderExcluirSó isso. Não tem que somar com o ''gamma recipiente '' ?
acho que tem sim!!! ta faltando um pedaço, acredito.
Excluiré só aplicar na fórmula do gama real, da 62x10^-6
ExcluirA resposta da segunda questão não seria: 6,2.10^-5?
ResponderExcluirA resposta da segunda questão não seria: 6,2.10^-5?
ResponderExcluir